본 글에서는 위에서 설명한 유한체적법을 이용하여 유체유동을 해석하기 위한 Navier-Stokes 방정식을 이산화하는 과정을 간략하게 요약하겠습니다. Navier-Stokes 방정식에 관한 아래 기사를 참조할 수 있습니다.
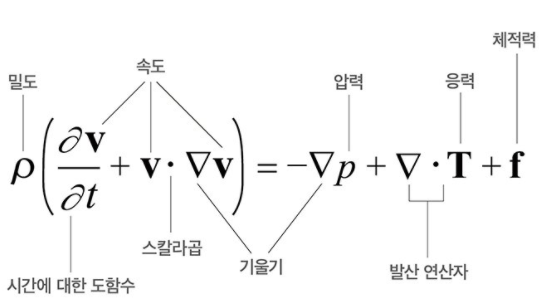
(유체역학) 8. 나비에-스토크스 방정식(Navier-Stokes Equation) – 유체의 운동량 보존 이 글은 다양한 유체역학 응용분야(자연과학뿐만 아니라 기계, 항공, 화학공학, 해양, 토목공학, 환경, 등)… blog.naver.com

Navier-Stokes 방정식에 유한체적법 적용

다음의 2차원 Navier-Stokes 방정식으로 시작하여 2차원 직교 격자를 가정해 보겠습니다.

Del 연산자(∇)를 이용하여 다시 쓰면 다음과 같다.
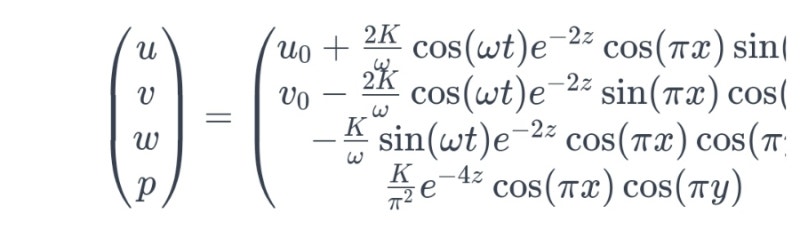
각 용어를 볼륨별로 통합합니다. (편의상 x축 방향만 요약하겠습니다.) 발산 정리를 적용합니다. 위에서 첫 번째 항은 다음과 같이 정리할 수 있다. 두 번째 용어는 다음과 같이 구성됩니다. 세 번째 용어는 다음과 같이 구성됩니다. 네 번째 용어는 다음과 같이 구성된다. x 및 y 방향 모두에 대한 최종 방정식은 다음과 같습니다. 미지수 u와 v와 계수 A로 정리하면 아래와 같은 형식을 취합니다. 또한 연속방정식은 다음과 같이 별도로 표현할 수 있다. 에필로그 마지막으로 (환경수치분석)이라는 카테고리를 마무리하고 싶습니다. 끝이 가까워질수록 조급함을 느껴 대충 마무리했지만, 개인적인 공부 과정의 기록으로 끝까지 정리한 것만으로도 의미가 있었다고 할 수 있습니다. 아무튼 완벽하지는 않아도 완성했다고 생각하니 뿌듯하네요~ㅎ (주의) ※ 아직은 끝없이 배우는 중이라 글에 오류나 오타가 있을 수 있습니다. ※ 해당 분야에 대해 궁금한 점이 있으신 경우, 정확한 정보가 필요하신 경우, 각종 교과서나 논문 등 신뢰할 수 있는 출처의 자료를 활용하시길 권장드립니다.